الإنحدار الخطي المتعدد باستخدام البرنامج الإحصائي SPSS
الإنحدار الخطي المتعدد
Multiple Linear Regression
مفهومــه .....ونموذج مطبق باستخدام البرنامج الإحصائي SPSS
إعداد
الأستاذ الدكتور ثائر داود سلمان
فرع العلوم النظرية - كلية التربية الرياضية / جامعة بغداد
يعد الإنحدار الخطي المتعدد من الأساليب الإحصائية
المتقدمة والتي تضمن دقة الإستدلال من أجل تحسين نتائج البحث عن طريق الإستخدام
الأمثل للبيانات في إيجاد علاقات سببية بين الظواهر موضوع البحث .
والإنحدار الخطي المتعدد هو عبارة عن إيجاد معادلة رياضية تعبر عن العلاقة بين متغيرين وتستعمل لتقدير قيم سابقة ولتنبؤ قيم مستقبلية ، وهو عبارة أيضاً عن إنحدار للمتغير التابع (Y) على العديد من المتغيرات المستقلة X1 , X2 , ...XKلذا فهو يستخدم في التنبؤ بتغيرات المتغير التابع الذي يؤثر فيه عدة متغيرات مستقلة أي تعتمد فكرته على العلاقات الدلالية التي تستخدم ما يعرف بشكل التشتت أو االانتشار ، فبإمكاننا التنبؤ بالمستوى الرقمي في فعالية رمي المطرقة على سبيل المثال إعتمادا ً على دراسة حالات أخرى للرامي كالعمر الزمني والعمر التدريبي والمهارة والمواصفات الجسمية وغيرها .
إن الإنحدار الخطي المتعدد ليس مجرد أسلوب واحد وإنما مجموعة من الأساليب التي يمكن أستخدامها لمعرفة العلاقة بين متغير تابع مستمر وعدد من المتغيرات المستقلة التي عادة ً ما تكون مستمرة)
والمعادلة الخطية في الإنحدار الخطي المتعدد هي :
Y = a + b1X1 + b2X2 + ……… + e
حيث أن Y = المتغير التابع
a = قيمة ثابتة Constant أوIntercept
b1= ميل ألإنحدار yعلى المتغير المستقل الأول
b2 = ميل ألإنحدار yعلى المتغير المستقل الثاني
1X =المتغير المستقل الأول
2X =المتغير المستقل الثاني
ويمكن استخدام الإنحدار الخطي المتعدد في حالة توافر الشروط التالية :
1.أن تكون العلاقة خطية بين المتغيرات المستقلة والمتغير التابع .
2.أن تكون البيانات موزعة توزيعا ً طبيعيا ً للمتغيرات المستقلة والمتغير التابع .
3.يجب أن تكون قيم المتغير التابع من المستوى الترتيبي على الأقل .
بعد الحصول على نتائج معادلة الانحدار يجب علينا أن نبين هل أن هذه المعاملات مقبولة من الناحية الإحصائية أي معنوية احصائياً مع التنويه بأن المعنوية تكون لكل معامل على حدة .
ولكي نحكم على معنوية معاملات الإنحدار نستعين باختبارT ومستوى الاحتمالية المقابل له وبالطبع فإن برنامج SPSS سيقوم تلقائياً باستخراج اختبار Tومستوى الاحتمالية المقابل له .
كما سيتم الحصول على إحصائيات تستخدم لمعرفة المعنوية الإجمالية للنموذج ومنها (R) ، ( R2 ) ، ( R2- ) .
فالأول Rهو معامل الأرتباط البسيط والذي يقيس قوة العلاقة بين متغيرين أو أكثر ، أما R2فهو يسمى بمعامل التحديد والذي يستخدم لمعرفة القوة التفسيرية للنموذج المقدر ( المعادلة المقدرة ) في حالة الإنحدار الخطي البسيط ( متغير مستقل واحد مع متغير معتمد واحد ) ، أما R2- فهو يستخدم لتفسير القوة التفسيرية لنموذج الانحدار الخطي المتعدد ( لأنه يأخذ بنظر الاعتبار عدد المتغيرات المستقلة ولذلك يسمى بالمصحح لأنه بالأصل مشتق من R2) .
كما نستخدم أيضا ً أحصائية F للحكم على معنوية النموذج المقدر ككل عند مستوى معنوية معين .
التطبيق العملي باستخدام البرنامج الاحصائي SPSS
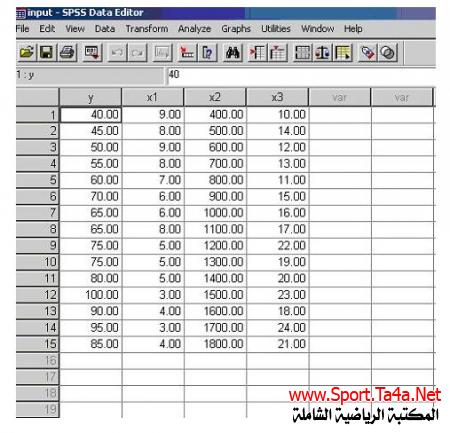
سأتناول المثال الموضح في الجدول التالي لإيجاد معادلة خط الإنحدار المتعدد للبيانات المعلقة بأختبار (15) طالبا ً إذ تمثل هذه البيانات العلاقة بين ( أختبار الوثب العريض من الثبات Y) والعوامل المؤثرة عليها وهي ( أختبار الشد لأعلى على العقلة X1 ) و ( أختبار السعة الحيوية X2 ) و ( أختبار الوثب العمودي من الثبات X3 ) ، وبإستخدام البرنامج الاحصائي SPSSسيتم الحصول على نتائج تقدير معادلة الانحدار الخطي المتعدد وكما يلي :
|
الوثب العريض من الثبات Y |
الشد لأعلى على العقلة X1 |
السعة الحيوية X2 |
الوثب العمودي من الثبات X3 |
|
40 |
9 |
400 |
10 |
|
45 |
8 |
500 |
14 |
|
50 |
9 |
600 |
12 |
|
55 |
8 |
700 |
13 |
|
60 |
7 |
800 |
11 |
|
70 |
6 |
900 |
15 |
|
65 |
6 |
1000 |
16 |
|
65 |
8 |
1100 |
17 |
|
75 |
5 |
1200 |
22 |
|
75 |
5 |
1300 |
19 |
|
80 |
5 |
1400 |
20 |
|
100 |
3 |
1500 |
23 |
|
90 |
4 |
1600 |
18 |
|
95 |
3 |
1700 |
24 |
|
85 |
4 |
1800 |
21 |
أولا ً / نقوم بادخال البيانات في محرر بيانات SPSS
ثانيا ً / نقوم بتسمية الأختبارات كما في الشكل الآتي
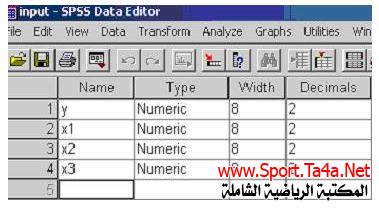
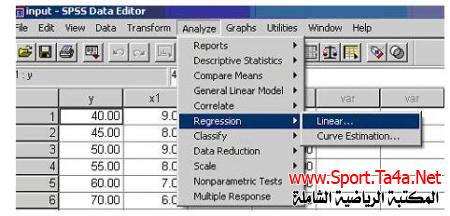
ثالثا ً / نذهب إلى قائمة analyzeونختار منها الأمر Regression ومن القائمة الفرعية نختار Linear ، كما في الشكل الاتي :
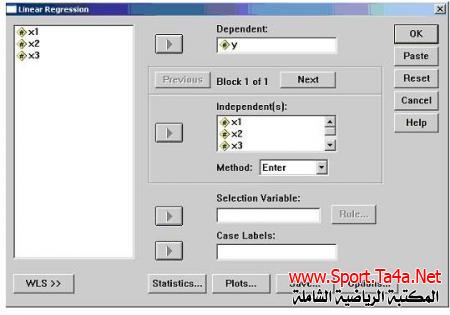
رابعا ً / من نافذة تحليل الإنحدار نقوم بتحديد المتغير التابع (Y) وننقله إلى خانة المتغير التابع ثم نحدد المتغيرات المستقلة وننقلها إلى خانة المتغيرات المستقلة ثم ننقر OK كما في الشكل الآتي :
خامسا ً / سوف نحصل على شاشة المخرجات الآتية :
Regression
تحليل النتائج التي تم الحصول عليها من SPSS
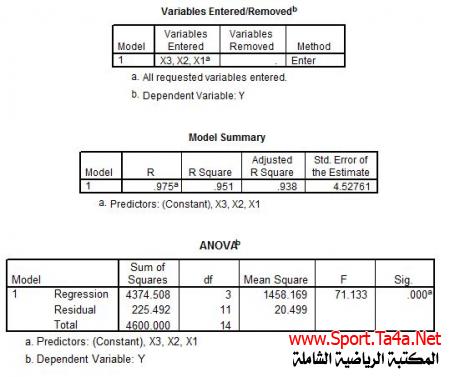
نستنتج من المخرجات أعلاه ما يلي :
-من الجدول الأول نلاحظ بأن طريقة الإنحدار المستخدمة وهي طريقة Enter حيث يتبين ان البرنامج قام بادخال جميع المتغيرات المستقلة في معادلة الإنحدار الخطي المتعدد .
-من الجدول الثاني نلاحظ بأن قيم معامل الارتباط الثلاثة وهي معامل الارتباط البسيط Rقد بلغ (0.975) بينما بلغ معامل التحديد R2(0.951 ) في حين كان معامل التحديد المصحح R2-(0.938) مما يعني بأن المتغيرات المستقلة التفسيرية ( أختبار الشد لأعلى على العقلة ، أختبار السعة الحيوية ، أختبار الوثب العمودي من الثبات ) استطاعت ان تفسر (0.94) من التغيرات الحاصلة في (أختبار الوثب العريض من الثبات) المطلوبة والباقي (0.06) يعزى إلى عوامل اخرى .
-كما يلاحظ في الجدول الثالث بأنه يتضمن قيم تحليل التباين والذي يمكن المعرفة من خلاله على القوة التفسيرية للنموذج ككل عن طريق إحصائية Fوكما يلاحظ من جدول تحليل التباين المعنوية العالية لأختبار F (P < 0.0001 ) مما يؤكد القوة التفسيرية العالية لنموذج الإنحدار الخطي المتعدد من الناحية الإحصائية .
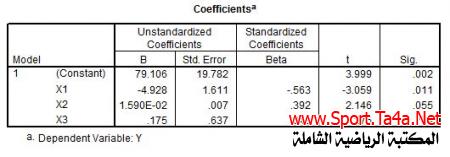
-أما في الجدول الرابع والأخير فيلاحظ قيمة الثابت ومعاملات الإنحدار ودلالتها الإحصائية للمتغيرات المستقلة على المتغير التابع ويمكن تلخيص هذه الجدول بالشكل الآتي :
المتغيرات المستقلة |
المتغير التابع |
|||
|
X3 |
X2 |
X1 |
Bالحد الثابت غير المعياري |
Y |
|
0.175 |
0.015 |
4.928- |
79.106 |
قيمة المعامل |
|
0.275 |
2.146 |
-3.059 |
3.999 |
قيم اختبار T |
|
0.789 |
0.055 |
0.01 |
0.002 |
المعنوية |
من الجدول نستنتج ان المتغيرات المستقلة ( أختبار الشد لأعلى على العقلة ) كان معنويا ً من الناحية الإحصائية وحسب أختبار t (عند مستوى معنوية P ≤ 0.05) ، في حين كاد ( أختبار السعة الحيوية ) أن يكون معنويا ً (عند مستوى معنوية P ≤ 0.05) إلا أن المتغير المستقل ( أختبار الوثب العمودي من الثبات ) لم يكن ذو تأثيرا ً معنويا ً في نموذج الإنحدار المتعدد وحسب أختبارt ، ومن الجدول الرابع والأخير يمكن التوصل إلى معادلات الإنحدار باستخدام Betaغير المعيارية ( الحد الثابت ) وكما يلي :
-إن معادلة خط إنحدار ( الوثب العريض من الثبات ) على أختبارات ( الشد لأعلى على العقلة والسعة الحيوية والوثب العمودي من الثبات ) هي :
الوثب العريض من الثبات = 79.106 + 4.928 × الشد لأعلى على العقلة + 0.015 × السعة الحيوية + 0.175 × الوثب العمودي من الثبات .
-تعد أوزان Betaالمعيارية ( الحد الثابت) هي معاملات المسار Path coefficients(تحليل المسار) حيث يمكن إيجاز تلك المعاملات فيما يلي :
-إدخال (أختبار الوثب العريض من الثبات ) كمتغير تابع وأختبارات ( الشد لأعلى على العقلة والسعة الحيوية والوثب العمودي من الثبات ) كمتغيرات مستقلة
الوثب العريض من الثبات = 0.563 ×الشد لأعلى على العقلة + 0.392 × السعة الحيوية + 0.043 × الوثب العمودي من الثبات .
وهذا السياق خطأ شاع في البحوث والدراسات النفسية والتربوية والإجتماعية إذ يتم استخدام Betaالمعيارية لإيجاد معادلات الإنحدار المفترضة .. لذا يجب أن يتم استخدام Betaغير المعيارية (الحد الثابت) .
طرق تطبيق الإنحدار الخطي Method :
هنالك خمسة خيارات أمام المستطيل المعنون Methodفي النافذة المعروضة في الفقرة (رابعا ً) حيث يمكن أختيار أحداها وفقا ً لمتطلبات العمل وكما يلي :
1.Enter : هذه الطريقة تم أستخدامها في المثال السابق وهي تستعمل عند أختيار إدخال كافة المتغيرات المستقلة مرة واحدة .
2.Stepwise : وهنا يتم إدخال المتغيرات المستقلة إلى المعادلة الخطية على خطوات ، ويتم أختيار متغيرين في الخطوة الأولى لإدخالهم إلى المعادلة ثم نقوم بإختيار المتغيرين وإقرار إمكانية أستبعادهما وحذفهما من المعادلة ، وفي كل خطوة ندخل متغيرين أثنين ويتم إتباع نفس الإجراءات .
3.Remove : يتم إدخال المتغيرات إلى المعادلة الخطية مرة واحدة حيث يتم حذف المتغيرات التي لا يمكن أرتباطها ذا دلالة إحصائية مرة واحدة .
4.Backward : يتم السير إلى الخلف بحيث تدخل المتغيرات جميعها مرة واحدة إلى المعادلة الخطية ثم يحذف المتغير المستقل الذي يكون لديه أدنى أرتباط جزئي مع المتغير التابع وهكذا حتى يبقى في المعادلة فقط المتغيرات المستقلة التي لها دلالة إحصائية .
5.Forward : عكس الطريقة السابقة حيث ندخل أولا ً المتغير الثابت وفي كل خطوة يتم إضافة المتغير الذي لديه أرتباط أعلى مع المتغير التابع وهكذا حتى نصل إلى الحد الذي لا تأتي عنه أي زيادة في معامل الإرتباط .
وإن أكثر الطرق شيوعا ً في التربية الرياضية هما طريقتي Enter و Stepwise .
 التعليقات: 0
التعليقات: 0
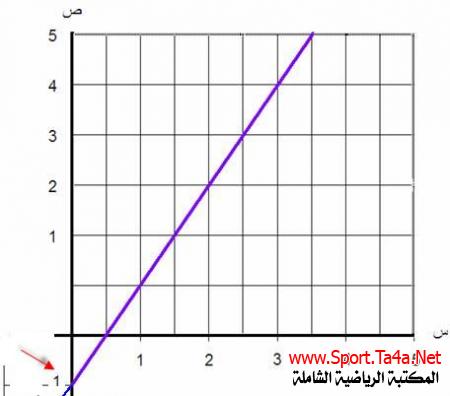
قراءة وتحليل العلاقة من رسم الانحدار الخطي البسيط
قراءة وتحليل العلاقة من رسم الانحدار الخطي البسيط خط الانحدار البسيط عبارة عن مستقيم يقطع المحور العمودي (ص او المتغير التابع) في احد الاتجاهين اما بالموجب او بالسالب ، ولتحليل الرسم يجب معرفة المعادلة والتي هي ( ص = أ + ب×س)...
تشخيص ومعالجة بعض الأخطاء الإحصائية في بحوث التربية الرياضية
تشخيص ومعالجة بعض الأخطاء الإحصائية في بحوث التربية الرياضية ذكر الله تعالى في كتابه الحكيم في قوله تعالى: بسم الله الرحمن الرحيم (ليعلم أن قد ابلغوا رسالات ربهم وأحاط بما لديهم واحصى كل شيء عدداً ) {الجن/28} صدق الله العظيم حيث...
التصنيف
التصنيــف يواجه الباحثون عادة عينة من المختبرين متعددة الخصائص فتصعب حينئذ عملية تحليل نتائج قياساتها اذ يعاب عليها عدم وجود التجانس وذلك لوجود فروق كبيرة بين صفات وسمات أفرادها ، لذلك يتم اللجوء إلى تقسيم أفراد العينة على فئات...
منهجية البحث وإجراءاته الميدانية
منهجية البحث وإجراءاته الميدانية يحدد الباحث الخطوات والإجراءات والطريقة والأسلوب الذي سوف ينتهجه في البحث . ويشمل : منهج البحث : يحدد الباحث الأسلوب او المنهج الذي سوف يستخدمه في إجراءات بحثه . سواء أكان المنهج وصفي ام تجريبي...
رسالة الموقع
نعتذر عزيزي مجموعة الـ الزوار غير مسموح لها باستخادم خاصية التعليقات .فضلاً قم بالتسجيل لتتمكن من التعليق على المواضيع
الموضوعات الأكثر مشاهدة
الكلمات الرئيسية
pdf الأداء الإنسان البحث البدنية التدريب التربية الجسم الحركة الحركي الحركية الرياضة الرياضي الرياضية العضلات العضلية الفرد القدم القلب القوة الكتاب الكرة اللاعب اللاعبين المدرب المهارات تحميل تدريب زيادة كتاب
| « أبريل 2024 » | ||||||
|---|---|---|---|---|---|---|
| أحد | أثنين | ثلاثاء | أربعاء | خميس | جمعة | سبت |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | |||||