المقذوفات في المجال الرياضي
المقذوفات في المجال الرياضي
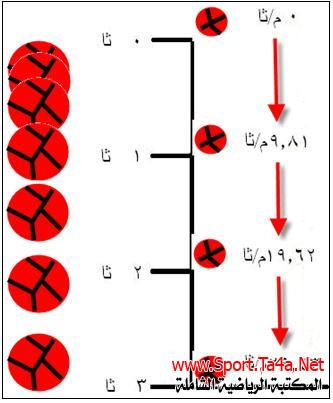
أي أداة أو جسم يكسر اتصاله مع شيء أخر وبزاوية معينة يسمى أو تسمى مقذوف ، فمثلا لاعب الوثب الطويل يكسر اتصاله مع لوحة الارتقاء في مرحلة الارتقاء بزاوية معينة وهنا نطلق على اللاعب مصطلح مقذوف ، كذلك عند المناولة في كرة السلة او الاعداد في الكرة الطائرة فان الاداة يكسر اتصاله مع يد اللاعب فتسمى الكرة مقذوف ، ولايختلف الموضوع كثيرا عندما يطلق الحكم في بداية الشوط كرة السلة الى الاعلى فان الكرة ستنطلق إلى الأعلى بزاوية قائمة (الطيران الحر) وبسرعة معينة تتباطأ وتتوقف ثم تبدأ بالرجوع بتسارع إلى نقطة انطلاقها او نقطة اعلى من نقطة انطلاقها (السقوط الحر) وكذلك يحدث عند لاعب الترامبولين واللاعب الذي يؤدي مهارة الضرب الساحق بالكرة الطائرة والفرد الخاضع لاختبار سارجنت (الوثب العمودي) ، ان هذا العمل بشكل بسيط سيقع تحت تأثير قانون الجذب ، والذي ينص على ان الأداة أو الجسم يسقط في الفراغ بتعجيل ثابت مقداره (9.81) متر في الثانية لكل ثانية، ومثلما أسلفنا سابقا فان كرة السلة عند سقوطها من السكون فان سرعتها ستبلغ بعد ثانية واحدة (9.81)م\ثا وفي الثانية الثانية تصبح سرعتها (9.81+9.81=19.62) ، فلو استغرقت الكرة عند سقوطها زمنا قدره (3 تانية) فانها ستصدم الأرض بسرعة مقدارها (29.43 م\ثا). وفقا للقانون:
|
|
|
|
|
الجذب |
= |
ـــــــــــــ |
|
|
|
الزمن |
|
|
|
|
|
الجذب |
= |
ـــــــــــــ |
|
|
|
الزمن |
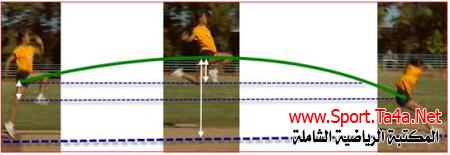
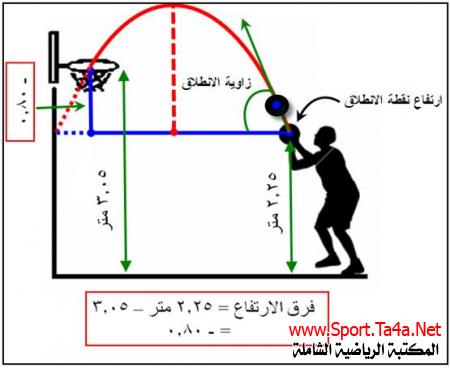
والمقذوفات بزوايا اقل من القائمة تحدث في شكلين اولهما تساوى نقطتي الانطلاق والهبوط والاخر تباين النقطتين ففي تباين النقطتين قد تكون نقطة الانطلاق اعلى من نقطة الهبوط مثلما يحدث في دفع الثقل او رمي الرمح او قد تكون نقطة الانطلاق ادنى من نقطة الهبوط كما يحدث في التصويب بكرة السلة وان فرق الارتفاع يحسب (ارتفاع نقطة الانطلاق – ارتفاع نقطة الهبوط) لذلك فاننا نتوقع ان يكون فرق الارتفاع في الحالة الاولى (دفع الثقل) بالموجب الا انه في الحالة الثانية (التصويب بكرة السلة) فان فرق الارتفاع يكون بالسالب.
وأدناه مجموعة من النقاط التي يمكن ملاحظتها على المقذوفات بزوايا مثل ركل كرة القدم أو رمي الرمح أو أداء الوثب الطويل وغيرها.
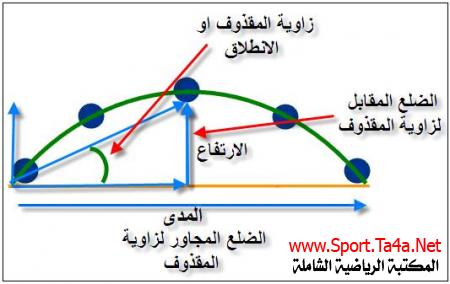
1-أي مقذوف يمتلك مصطلحين أولهما (المدى) ويقصد به المسافة الأفقية لمسار المقذوف ، والمصطلح الأخر هو (الارتفاع) ويقصد به المسافة العمودية للمقذوف.
2-لكل من المصطلحين زمنين مختلفين فزمن الوصول إلى أقصى ارتفاع (المسافة العمودية) يختلف عن الزمن الكلي الذي استغرقه المدى أو المسافة الأفقية أو زمن الطيران.
3-ان العلاقة بين المسافة والزمن تحكمها مصطلح السرعة ، وبذلك فان
|
المسافة الأفقية أو العمودية |
= |
السرعة المحصلة × زمن المسافة الأفقية أو العمودية |
4-مصطلح الجذب الأرضي يتعامل مع الارتفاع العمودي وليس له علاقة بالمدى أو المسافة الأفقية.
5-طالما ان الارتفاع العمودي أو السرعة العمودية تحددها الجذب الأرضي فأن زمن الوصول الى اقصى ارتفاع (الارتفاع العمودي) يتم حسابه بوجود الجذب الأرضي.
6-ان الارتفاع العمودي هو الضلع المقابل لزاوية المقذوف وبذلك فان المسافة العمودية او السرعة العمودية تعامل مع جيب الزاوية.
7-ان المدى الأفقي هو الضلع المجاور لزاوية المقذوف وبذلك فان المسافة الافقية او السرعة الافقية تعامل مع جيب تمام الزاوية.
8-يتم حساب أقصى ارتفاع يصله المقذوف من خلال القانون الأتي
|
|
|
(السرعة × جيب الزاوية)2 |
|
أقصى ارتفاع |
= |
ـــــــــــــــــــــــــــــــــــــــــــــ |
|
|
|
2 × الجذب |
9-يتم حساب زمن الوصول إلى أقصى ارتفاع يصله المقذوف من خلال القانون الأتي:
|
|
|
السرعة × جيب الزاوية |
|
زمن الوصول إلى أقصى ارتفاع |
= |
ـــــــــــــــــــــــــــــــــــــــ |
|
|
|
الجذب |
10-من المتوقع ان أقصى ارتفاع يكون في منتصف المدى على اعتبار ان للمقذوف مسار على شكل قطع مكافئ ، وعليه فأن زمن طيران الأداة يحسب من الفقرة (9) وذلك بضربها في (2) وهو زمن المسافة الافقية أو الطيران. وعليه فان الزمن يحسب وفقا للقانون ادناه
|
|
|
|
السرعة × جيب الزاوية |
|
زمن الطيران او المسافة الافقية |
= |
2 × |
ـــــــــــــــــــــــــــــــــــــــ |
|
|
|
|
الجذب |
او
زمن الطيران او المسافة الافقية = 2 × زمن الوصول الى اقصى ارتفاع
11-يتم حساب المسافة الأفقية وفقا للقانون ادناه:
|
المسافة الأفقية |
= |
السرعة المحصلة × جيب تمام زاوية المقذوف × الزمن الكلي |
12-عندما تكون زاوية المقذوف (90 درجة) فان قيمة جيب الزاوية هي (1) وعندما تكون زاوية المقذوف (45) درجة فان قيمة جيب الزاوية (0.5) لذلك فان أي قيمة نضربها في جيب الزاوية (90) تبقى مثلما هي اما عند ضربها في جيب الزاوية (45) فان القيمة تقل الى النصف ، وعليه فان افضل زاوية للحصول على افضل مسافة افقية محسوبة بـ (2× جيب الزاوية) .
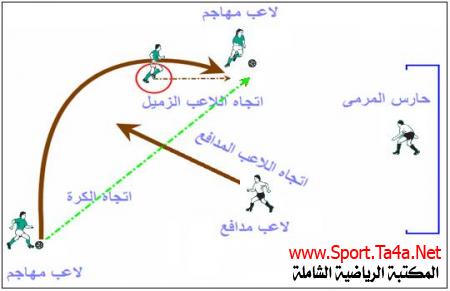
مثال :في الشكل ادناه لاعب مهاجم يحاول ان يعطي مناولة عالية الى زميله وهذا يعني ان الكرة ستصبح مقذوفا أي بحاجة الى سرعة وزاوية ، ولان اللاعبين في حالة هجوم فان زميله في حالة حركة الى الامام وفي الوقت نفسه فان لاعب مدافع قد اكتشف خطة المناولة وهو في منتصف المسافة بين اللاعبين المهاجمين فتحرك لحظة المناولة لقطع مسار الكرة فلو افترضنا ان اللاعب المدافع سيقطع مسار الكرة في منتصف المسافة أي يحتاج الى التوقيت المناسب وهذا يتطلب معرفة زمن وصول الكرة لاقصى ارتفاعها ، ومن ناحية اخرى فان المطلوب من اللاعب المهاجم الذي سيستلم الكرة اما القفز لاستلام الكرة بالرأس او الصدر لان مسار الكرة عالي او الاكتفاء بتسكين الكرة بالرجل والاستمرار . فلو بلغت السرعة الابتدائية للكرة (12 م\ثا) وبزاوية (35 درجة) . .باهمال مقاومة الهواء وسرعة الريح جد ما مطلوب من اللاعبين المدافع والمهاجم كتصرف تجاه الموقف؟
ملاحظة: ان هذا الحدث حقيقي وان اللاعبين يتصرفون وفقا لادراكهم الحسي للزمن والمسافة وان افتراض تواجد اللاعب المدافع في الوسط او قريبا من اللاعب المهاجم الذي يناول الكرة او قريبا من اللاعب المهاجم الذي يستلم الكرة افتراض ميداني يتصرف المدافع بشكل مختلف في كل موقع. اللاعب المهاجم الذي سيستلم الكرة بالرأس او بالصدر سيقلب القانون الى مقذوفات بتباين مستويات الانطلاق والهبوط ونفترض الاستلام بالقدم.
|
|
|
(السرعة × جيب الزاوية)2 |
|
أقصى ارتفاع |
= |
ـــــــــــــــــــــــــــــــــــــــــــ |
|
|
|
2 × الجذب |
|
|
|
(12 × 0.5736)2 |
|
أقصى ارتفاع |
= |
ــــــــــــــــــــــــــــــ |
|
|
|
2 × 9.81 |
|
|
|
(12 × 0.5736)2 |
|
أقصى ارتفاع |
= |
ــــــــــــــــــــــــــــــ |
|
|
|
2 × 9.81 |
|
أقصى ارتفاع |
= |
2.41 متر |
المطلوب من اللاعب المدافع ان يرتفع اعلى من (2.41 متر) لقطع مسار الكرة |
|
|
|
السرعة × جيب الزاوية |
|
زمن الوصول إلى أقصى ارتفاع |
= |
ـــــــــــــــــــــــــــــــــــــــ |
|
|
|
الجذب |
|
|
|
12 × 0.5736 |
|
زمن الوصول إلى أقصى ارتفاع |
= |
ــــــــــــــــــــــــــــــ |
|
|
|
9.81 |
|
زمن الوصول إلى أقصى ارتفاع |
= |
0.70 ثانية |
المطلوب من اللاعب المدافع ان يصل خلال اقل من (0.70 ثانية) لأقصى ارتفاع للكرة |
|
الزمن الكلي (للمسافة الأفقية) |
= |
0.70 × 2 |
|
الزمن الكلي (للمسافة الأفقية) |
= |
1.40 ثانية |
المطلوب من اللاعب الزميل ان يصل الى المكان المتوقع لتواجد الكرة خلال (1.40 ثانية) |
|
المسافة الأفقية |
= |
السرعة المحصلة × جيب تمام زاوية المقذوف × الزمن الكلي |
|
المسافة الأفقية |
= |
12 × 0.8192 × 1.40 |
|
المسافة الأفقية |
= |
13.76 متر |
الكرة ستقطع مسافة فدرها (13.76 مترا) هل هذه مسافة كافية لكي يستلم الزميل الكرة دون مشاكل من اللاعب المدافع |
|
|
|
13.76 متر |
|
اللاعب المهاجم الذي سيستلم الكرة يجب ان يتحرك من مكانه الى الموقع المتوقع لسقوط الكرة بمقدار السرعة الناتجة اذا كان مبتعدا بالمقدار نفسه من ابتعاد اللاعب المهاجم الذي ناول الكرة من موقع سقوط الكرة ، وبما ان المسافة اقل فتكون السرعة المقدرة بالنسبة والتناسب وهذا يتطلب من اللاعب المهاجم ووفقا للتكنيك المطلوب تقدير مسافة وزمن وصول الكرة بالإدراك الحسي الحركي للمسافة والزمن |
|
معدل سرعة الكرة |
= |
ــــــــــــــــــــــ |
9.83 م\ثا |
|
|
|
|
1.40 ثانية |
|
تباين مستويات الانطلاق والهبوط
عند تباين مستويات الانطلاق والهبوط يخرج مسار الكرة من شكل القطع المكافئ لذلك تم معالجة ذلك وحسب الخطوات ادناه
1-حساب الزمن: يتم وفقا للقانون في الفقرة (10) مع بعض التعديلات :
|
|
|
|
|
|
|
|
|
السرعة × جيب الزاوية + |
|
(السرعة × جيب الزاوية)2+ (2 × الجذب × فرق الارتفاع) |
|
الزمن الكلي |
= |
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ |
||
|
|
|
الجذب |
||
ان القانون اعلاه يصلح حتى اذا كان فرق الارتفاع صفرا أي ان مستوى الانطلاق يساوي مستوى الهبوط
2-يتم حساب المسافة وفقا للقانون في الفقرة (11)
|
المسافة الأفقية |
= |
السرعة المحصلة × جيب تمام زاوية المقذوف × الزمن الكلي |
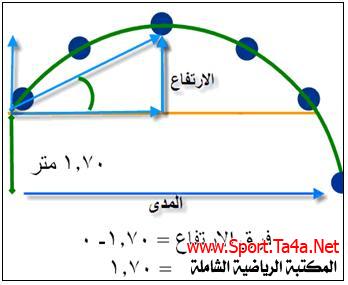
الشكل مثال في دفع الثقل

الشكل مثال في التصويب بكرة السلة
 التعليقات: 0
التعليقات: 0
الحركات الرياضية بين النموذج والمثالي
الحركات الرياضية بين النموذج والمثالي تعتمد العلوم في المجال الرياضة على القيم الرقمية أو الرسوم البيانيـة الناتجـة مـن تحليل البيانات أو المعطيات التي تم استحصالها من المهارة ، وعلى الأغلب فان شكل المهارة عبارة عن مسارات شكل...
ركلة الجزاء من وجهة نظر البيوميكانيك
ركلة الجزاء من وجهة نظر البيوميكانيك تعتبر ركلة الجزاء من العقوبات المهمة التي تعطى للفريق المهاجم فهي من الاخطاء العشرة التي تعتبر عقوبتها القانونية ركلة حرة مباشرة وبما ان حدوثها داخل منطقة الجزاء فيتعامل معها الحكم كركلة جزاء...
البناء الحركي للمهارات الرياضية
البناء الحركي للمهارات الرياضية البناء الحركي (مراحل الحركة الرياضية ):- لانجاز مهارة أو حركة أو واجب حركي معين نجد أن الجسم يمر بمراحل تساعده على تأدية الحركة وبنظرة عامة إلى الحركات الرياضية نجد أنها غير متماثلة في المراحل التي...
علم الميكانيك
علم الميكانيك -المقدمة: يعد علم الميكانيك احد فروع علم الفيزياء الذي يهتم بدراسة القوانين والعوامل الميكانيكية ذات التأثير في حركة الكائنات الحية,وبما أن الحركة الرياضية وأدائها الفني يتطلب وبشكل كبير إلى زيادة معرفة القوانين...
رسالة الموقع
نعتذر عزيزي مجموعة الـ الزوار غير مسموح لها باستخادم خاصية التعليقات .فضلاً قم بالتسجيل لتتمكن من التعليق على المواضيع
الموضوعات الأكثر مشاهدة
الكلمات الرئيسية
pdf الأداء الإنسان البحث البدنية التدريب التربية الجسم الحركة الحركي الحركية الرياضة الرياضي الرياضية العضلات العضلية الفرد القدم القلب القوة الكتاب الكرة اللاعب اللاعبين المدرب المهارات تحميل تدريب زيادة كتاب
| « يوليو 2024 » | ||||||
|---|---|---|---|---|---|---|
| أحد | أثنين | ثلاثاء | أربعاء | خميس | جمعة | سبت |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | ||||